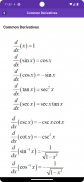
Calculus Formulas

A kalkulus magában foglalja a „folyamatos változás” tanulmányozását és alkalmazását az egyenletek megoldásában. Két fő ága van:

1:

Differenciálszámítás

, amely a változási sebességre és a görbék lejtőire vonatkozik.

2:

Integrált kalkulus

a mennyiségek felhalmozódására, valamint a görbék alatti és azok közötti területekre.

Mind a differenciális, mind az integrált kalkulus felhasználja a végtelen szekvenciák és a végtelen sorozat konvergenciájának alapvető fogalmait egy jól meghatározott határig. Ez a két ág kapcsolódik egymáshoz a kalkulus alaptétele szerint

A differenciális kalkulus egy területet kis részekre oszt fel, hogy kiszámítsa a változás sebességét. Míg az integrált kalkulus kis részekkel egyesíti a területet vagy a térfogatot. Röviden: ez az érvelés vagy a számítás módszere.

Ebben az alkalmazásban megtekintheti a kalkulus-képletek listáját, például integrálképlet, származékos képlet, határérték-formula stb.

A korlátozási képletek a következőket tartalmazzák:

Határozatok meghatározásai.

A határ és az egyoldalú határ közötti kapcsolat.

Korlátozza a tulajdonságok képleteit.

Alapvető határértékelési képletek.

Értékelési technikák képletei.

Néhány folyamatos funkció.

Köztes érték tétel.

Oldja meg a kalkulus korlátját.

A származékos képletek a következőket tartalmazzák:

Származékos termékek meghatározása és jelölése.

A származék értelmezése.

Alapvető tulajdonságok és képletek.

Közös származékok.

Láncszabály variánsok.

Magasabb rendű származékok.

Implicit differenciálás.

Növelés / csökkentés - konkáv fel / konkáv le.

Extrema.

Átlagos érték tétel.

Newton-módszer.

Kapcsolódó árak.

Optimalizálás .

Az integrált képletek a következőket tartalmazzák:

Integrális meghatározások.

A kalkulus alaptétele.

Tulajdonságok.

Közös integrálok.

Standard integrációs technikák.

Nem megfelelő integrál.

Meghatározó integrálok megközelítése.

Nagyon praktikus alkalmazás a matematika hallgatói számára.